The concept of chaos might suggest complete randomness, but to scientists, it denotes systems that are so sensitive to initial conditions that their output appears random, obscuring their underlying internal rules of order: the stock market, rioting crowds, brain waves during an epileptic seizure, or the weather. In a chaotic system, tiny effects are amplified through repetition until the system goes critical. The roots of today's chaos theory rest on a serendipitous discovery in the 1960s by mathematician-turned-meteorologist Edward Lorenz.
These scientists created jewelry out of the striking shapes of chaos theory
Not just inspired by chaos theory, but directly created from its mathematical principles.

Chaotic shapes 3D-printed in bronze represent the first step in the transformation from chaos to manufacturable forms.
F. Bertacchini/P.S. Pantano/E. Bilotta
"A team of Italian scientists has figured out a way to turn the striking, complex twisting shapes of chaos theory into actual jewelry, according to a new paper published in the journal Chaos. These pieces aren't simply inspired by chaos theory; they were directly created from its mathematical principles.
"Seeing the chaotic shapes transformed into real, polished, shiny, physical jewelry was a great pleasure for the whole team. Touching and wearing them was also extremely exciting," said co-author Eleonora Bilotta of the University of Calabria. "We think it is the same joy that a scientist feels when her theory takes form, or when an artist finishes a painting."
. . .Lorenz thought the advent of computers provided an opportunity to combine mathematics and meteorology for better weather prediction. He set out to construct a mathematical model of the weather using a set of differential equations representing changes in temperature, pressure, wind velocity, and the like. Once he had his skeleton system, he kept a continuous simulation running on his computer, which would produce a day’s worth of virtual weather every minute. The resulting data resembled naturally occurring weather patterns—nothing ever happened the same way twice, but there was clearly an underlying order.
One wintry day early in 1961, Lorenz decided to take a shortcut. Instead of starting the whole run over, he started midway through, typing the numbers straight from an earlier printout to give the machine its initial conditions. Then he walked down the hall for a cup of coffee. When he returned an hour later, he found that, instead of exactly duplicating the earlier run, the new printout showed the virtual weather diverging so rapidly from the previous pattern that, within just a few virtual “months,” all resemblance between the two had disappeared.
Six decimal places were stored in the computer’s memory. To save space on the printout, only three appeared. Lorenz had entered the shorter, rounded-off numbers, assuming that the difference—one part in a thousand—was inconsequential, similar to a small puff of wind that is unlikely to have much impact on large-scale features of the weather. But in Lorenz’s particular system of equations, such small variations proved catastrophic.
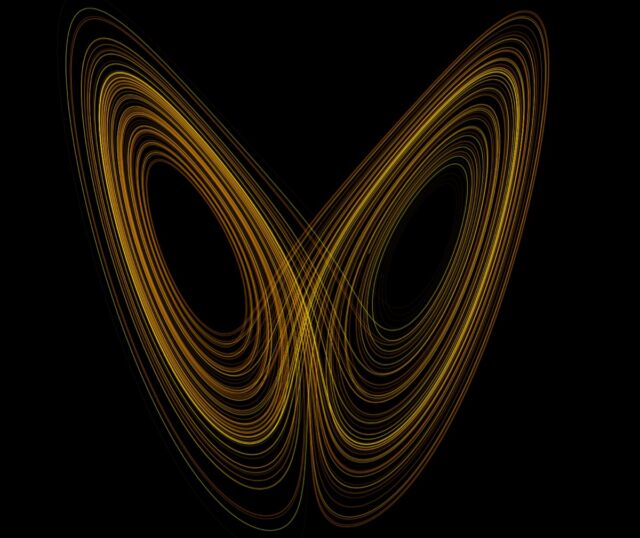
✓ This is known as sensitive dependence on initial conditions. Lorenz subsequently dubbed his discovery “the butterfly effect”: The nonlinear equations that govern the weather have such an incredible sensitivity to initial conditions—that a butterfly flapping its wings in Brazil could theoretically trigger a tornado in Texas. The metaphor is especially apt. To investigate further, Lorenz simplified his complex weather model, focusing on rolling fluid convection in our atmosphere: basically, a gas in a solid rectangular box with a heat source on the bottom and cooled from above, in which warm air rises to the top and cooler air sinks to the bottom. He simplified a few fluid dynamics equations and found that plotting the results of specific parameter values in three dimensions produced an unusual butterfly-shaped figure.
✓ It's called a strange attractor. In a linear dynamic system, an attractor is a component that makes it more likely that other system components will come closer to a specific point, ultimately finding a stable configuration that is less sensitive to minor perturbations. The classic example of an attractor is the lowest point in the arc of a damped pendulum (i.e., with friction). With a strange attractor, however, you never know exactly where that point will be. And strange attractors are non-periodic, meaning the system's motion never repeats exactly.
Lorenz may have discovered the first strange attractor, but it was Leon O. Chua who introduced Chua's circuit in 1983: a simple electronic circuit design that produces an oscillating waveform that never repeats. It was later variations on Chua's circuit that inspired the chaotic jewelry created by Bilotta and her co-authors. "These chaotic configurations are complex structures that had never been observed before," said Bilotta. "The depictions of such [strange attractors] are strikingly beautiful, continually shifting when the point of view is changing. Jewelry seemed to be the best way to interpret the beauty of chaotic shapes."
F. Bertacchini et al., 2023
Earrings and necklace made with different attractors. They were cast and finished with traditional methods by a craftsman using a cast.
The first phase was to create a simulation of the various attractors so that users could explore different parameters to choose their desired shape—essentially enabling them to "make exclusive and mathematically encoded jewelry," per the authors.
> A 3D printer file was produced based on the chosen shape and sent to the printer to make a resin-molded model, thereby capturing all the necessary detail and structure. The mold was then sent to a goldsmith, who produced the final metal print. The computational system is automated to allow quick prototyping of single shapes, which can then be connected to make rings, necklaces, earrings, or bracelets. Some sample jewelry is featured in the gallery above."
X










No comments:
Post a Comment